SLAM最小二乘问题

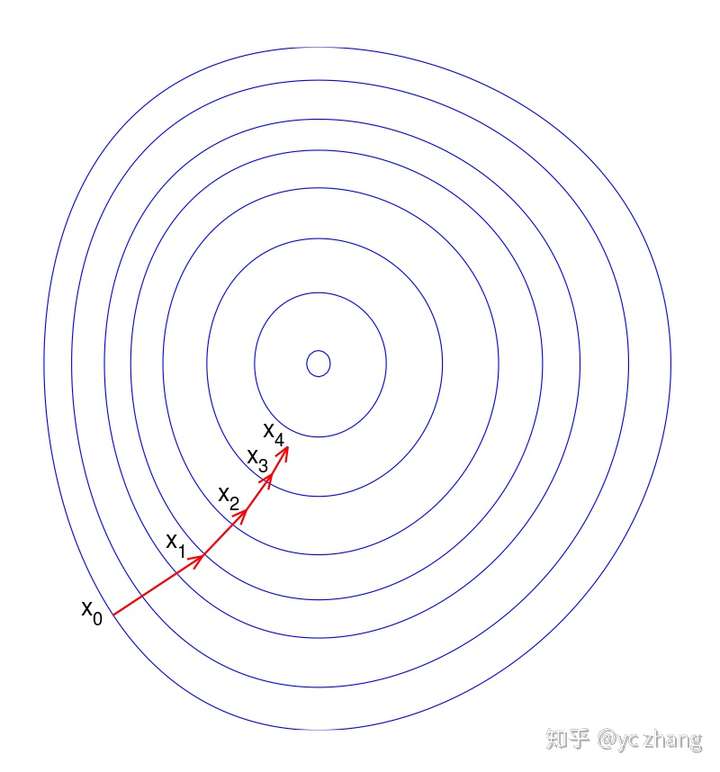
在SLAM的过程中，我们可以构建机器人状态过程。通过对其概率的计算，最终将问题转化为了求最大似然估计的问题。

最小二乘问题

我们想要求解的问题是SLAM过程中的最大似然估计问题。由于最大似然估计问题可以转换为最小二乘问题，所以也就是最小二乘的求解问题。我们假设目标函数为 $F(x)$ ，误差函数为 $f(x)$ ，则其最小二乘可以表示为[1]：

$minF(x)=\frac{1}{2}||f(x)||^2_2$

那么如何求解这个问题呢？常规的思路就是对目标函数 $F(x)$ 进行求导，当其导数为0的时候，求 $x$ 的最优解，最终求得极值，这里需要注意导数为0的点，不一定就是极值点，可能会是鞍点。然而，有些时候，若目标函数 $F(x)$ 的不是很容易进行求导，这个时候就需要使用一些迭代的方法，来使得目标函数 $F(x)$ 下降，这样就可以逐步迭代，求得最小值了。整个的迭代流程如下所示：

给定某个初始值$x_0$;
对于第$k$次迭代,寻找一个增量 $\Delta x_k$ ,使得误差$||f(x_k+\Delta x_k)||_2^2$ 达到极小值;
若 $\Delta x_k$ 足够小,则停止迭代;
否则,令$x_{k+1}=x_k+\Delta x_k$,返回第2步.

因此，上诉问题，就变成了不断寻找下降增量 $\Delta x_k$ 的问题。为了方便求解，我们只需要关心误差函数 $f(x)$ 在迭代值处的局部性质，而不用考虑 $F(x)$ 在迭代值处的全局性质，这种方法在最优化，机器学习领域使用的非常广泛。

求解最小二乘方法

梯度下降法
牛顿法
高斯牛顿法
LM法
序列二次规划SQP
信赖域方法
进化方法

牛顿法

说到优化方法，那自然不能少了最基本的牛顿法。牛顿法在本科的时候大家应该都学过，这里进行一下回顾：首先定义一个实变量 $x$ ，和其单变量函数 $f(x)$ ，函数的一阶导数记为 $f^{’}(x)$ ，二阶导数记为 $f^{’’}(x)$ [2]。那么首先看一个牛顿法最常用的场景——求根：

一元函数求根：

假设有根的近似解 $x_0$ ，则满足假设且更接近根的值为： $x_1=x_0-\frac{f(x_0)}{f^{’}x_0}$ 以此类推，可以得到： $x_{n+1} = x_n - \frac{f(x_n)}{f^{’}(x_n)}$

因此，根据上面的流程，可以逐步求得 $f(x)=0$ 的根。我们假设当前的近似解为 $x_n$ ，那么迭代之后的下一个解，列出当前的切线方程为： $y=f^{’}(x_n)(x-x_n)+f(x_n)$ 设定其在 $x$ 轴的截距为 $x_{n+1}$ ，将 $(x_{n+1},0)$ 代入方程，可以得到： $0=f^{’}(x_n)(x_{n+1}-x_n)+f(x_n)$

即： $x_{n+1}=x_n-\frac{f(x_n)}{f^{’}{x_n}}$

因此，我们得到了在函数 $f(x)$ 上求解 $f(x)=0$ 的方法。

求函数的极值：

我们在前面知道了求解函数的根的方法，那么和函数的极值有什么关系呢？我们知道函数的极值的必要条件是其一阶微分等于0。那么求解微分方程为0时候的值，从而函数的极值了。为了能够方便理解整个流程，我们还是拿一元函数 $f(x)$ 来举例。我们首先对其在 $x=x_0$ 处进行二阶泰勒展开：

$f(x)=f(x_0)+f^{’}(x_0)(x-x_0)+\frac{f^{’’}(x_0)}{2}(x-x_0)^2+\sigma(x-x_0)^2$

其中，由于泰勒展开的特性，后面 $\sigma(x-x_0)$ 部分不予考虑，我们只考虑前面展开部分的极值问题：

$g(x)=f(x_0)+f^{’}(x_0)(x-x_0)+\frac{f^{’’}(x_0)}{2}(x-x_0)^2$

上面的式子是一个一元二次函数，那么其极值就是一阶导数为0的时候，我们可以先微分：

$g^{’}(x)=f^{’}(x_0)+f^{’’}(x_0)(x-x_0)$

令 $g^{’}(x_1)=0$ ，则此时的 $x_1$ 就是极值（为了方便说明，暂不考虑鞍点的情况）。

故 $f^{’}(x_0)+f^{’’}(x_0)(x_1-x_0)=0$

$x_1=x_0-\frac{f^{’}(x_0)}{f^{’’}(x_0)}$

以此类推，可以得到迭代公式：

$x_{n+1}=x_n-\frac{f^{’}(x_n)}{f^{’’}(x_n)}$

根据这个方法就可以不断的迭代下去直到收敛，最终找到极值了。如果是多元的情况，则一阶导数 $f^{’}(x)$ 被叫做梯度，也称之为雅可比矩阵 $J$ [3]（这里不太严谨。严格来说，矩阵的梯度为一阶导的转置，函数的梯度为一阶导，这里并没有进行详细的区分），二阶导数矩阵 $f^{’’}(x)$ ，也被叫做海塞矩阵 $H$ [4]。如果是收敛的话， $\Delta x=x_{n+1}-x_n \approx 0$ ，则式子可以转化为：

$\Delta x = -\frac{f^{’}(x_n)}{f^{’’}(x_n)}=-\frac{J}{H}$

也就是说：

$H \Delta x=-J$

这样，就可以求出能够取得函数 $f(x)$ 的极值点，继而算出函数 $f(x)$ 的极值。

由于牛顿法需要算二阶导数，如果高阶的话，需要算海塞矩阵，这里是有三个缺陷： 1.要求给定的方程需要二阶可导 2.非凸函数的海森矩阵不一定有逆 3.数据较大的时候，海塞矩阵的计算量偏大因此，需要思考别的方法来进行最小二乘问题的优化和求解。

梯度下降法

为了能够更好的进行最值问题的优化求解，我们可以使用高斯牛顿法（GN）和列文伯格-马夸特法（LM）。再介绍上面两个方法之前，我们首先介绍一下梯度下降法[5]。梯度下降是用于找到可微函数的局部最小值的一阶迭代优化算法。为了使用梯度下降找到函数的局部最小值，我们采取与该数在当前点的梯度（或近似梯度）的负值成比例的步骤。

梯度下降法是基于以下的观测原理而来的：如果实值函数 $f(x)$ 在点 $x=a$ 处可微且有定义，那么函数 $f(x)$ 在点 $a$ 处，沿着梯度的反方向$-\Delta f(a)$ 下降的最快。因此，假设有个点 $b$ ，满足：

$b=a-\gamma \Delta f(a) \qquad s.t \qquad \gamma>0 \quad \& \quad r\to0$

那么我们就可以得到：

$f(a) \ge f(b)$

通过这种方法，就可以找到极小值。

因此，得到迭代公式：

$x_{n+1}=x_n - \gamma \Delta f(x_n)$

其中， $\gamma$ 是我们人为设定的参数，通过迭代，就可以得到极值。

梯度下降法每次都以梯度的反方向下降，所以，有可能会容易走出锯齿路线，从而增加迭代次数。

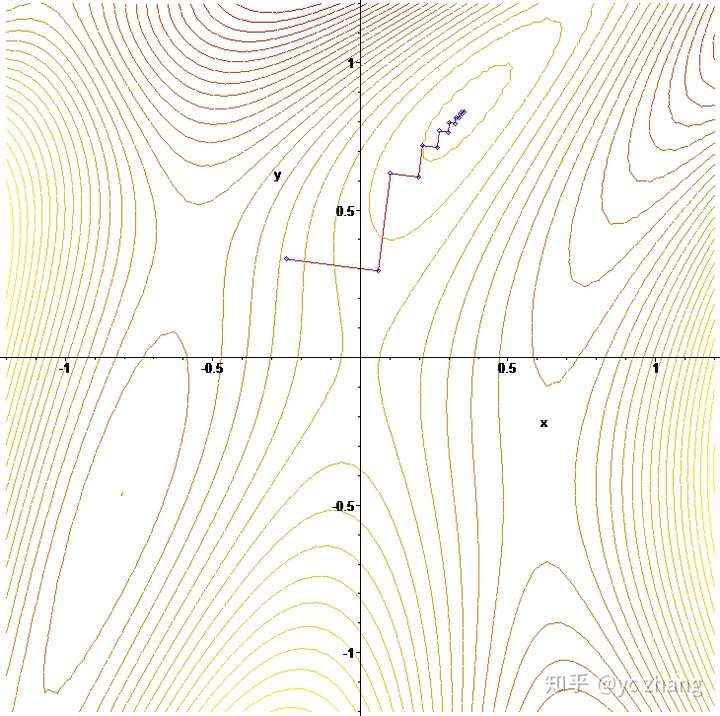
高斯牛顿法

如果代入到最小二乘问题中，牛顿法和梯度下降法都是针对目标函数 $F(x_k)$ 来进行求解的，这样，就不可避免的需要求得海塞矩阵 $H$ ，所以，为了避免这个问题，我们选取了误差函数 $f(x)$ 来进行优化求解：

$minF(x)=\frac{1}{2}||f(x)||^2_2$

那么，我们从上面的迭代步骤2中可以看到：

给定某个初始值$x_0$;
对于第 $k$ 次迭代,寻找一个增量$\Delta x_k$,使得误差 $||f(x_k+\Delta x_k)||^2_2$ 达到极小值;
若干 $\Delta x_k$ 足够小,则停止迭代;
否则,令$x_{k+1}=x_k+\Delta x_k$,返回第2步

那么，我们对 $f(x+\Delta x)$ 进行一阶泰勒展开。

$f(x+\Delta x) \approx f(x)+J(x)^T \Deltax+ \sigma(\Delta x)$

我们需要求 $\Delta x$ 使得上面的式子 $||f(x+\Delta x)||^2_2$ 有最小值，所以，我们可以得到最小二乘问题为：

$\Delta x^* = argmin \frac{1}{2}||f(x+\Delta x)||^2_2 \approx argmin \frac{1}{2}||f(x)+J(x)^T \Delta x||^2_2$

为了求极值，对其求导：

$m(x)=\frac{1}{2}||f(x)+J(x)^T \Delta x||^2 = \frac{1}{2}(f(x)+J(x)^T \Delta x)^T(f(x)+J(x)^T \Delta x)$

$=\frac{1}{2}(||f(x)||^2+2f(x)J(x)^T \Delta x + \Delta x^TJ(x)J(x)^T\Delta x)$

故，对其求导可以得到：

$m^{’}(x)=J(x)f(x)+J(x)J(x)^T\Delta x$

则，此时可以转化为线性求解问题：

$m^{’}(x)=0 \quad \to \quad J(x)J(x)^T\Delta x = -J(x)f(x)$

令 $J(x)J(x)^T$ 定义为 $H(x)$ ，令 $-J(x)f(x)$ 定义为 $g(x)$ ，则此时变为了：

$H\Delta x = g \qquad s.t \qquad H=JJ^T \quad \& \quad g=-Jf$

这样，就可以优化求解了。上面的最小二乘的优化步骤就可以变为[6]：

给定某个初始值$x$;
对于第 $k$ 次迭代,求出当前的雅克比矩阵$J(x_k)$ 和误差$f(x_k)$
求解增量方程:$H\Delta x_k = g$
若 $\Delta x_k$ 足够小,则停止迭代
否则,令$x_{k+1}=x_k+ \Delta x_k$ ,返回第2步

相比较于传统的最小二乘求解方法，只更改了两个步骤。该方法的优点和缺点如下：

优点：

避免了求海塞矩阵，大大减少了计算量。缺点：

为了求解 $H$ ，需要 $H$ 矩阵可逆，但是实际上 $JJ^T$ 只有半正定性，所以，当为奇异矩阵的时候，稳定性较差，算法不收敛。如果求出来的步长 $\Delta x_k$ 太大，会导致其局部近似不精确，严重的时候，可能无法保证迭代收敛。容易和梯度下降法一样，陷入锯齿状，导致迭代次数较长。不过，为了能够更好的进行最小二乘问题的求解，我们可以使用列文伯格-马夸特法(LM)来进行求解。

`列文伯格-马夸特法`

该方法是在高斯牛顿法的基础上进行的改进，基本的思路和原理和高斯牛顿法一样。

在高斯牛顿法的缺点中，可以看到，有一点使容易进入锯齿状，导致迭代的次数较长。所以，为了避免其步长过大导致的问题，该方法提出了信赖区域，设定一个区域。使得步长能够受到控制[7]。

在更新迭代的过程中，为了判定近似值的好坏，我们设定了一个评判指标：

$\rho = \frac{f(x+\Delta x)-f(x)}{J(x)^T\Delta x}$

这个指标就是我们的近似指标，可以看到其分为以下几种情况：

$\rho$ 接近1，近似是好的，不需要更改； $\rho$ 太小，则实际减少的值小于近似减少的值，近似较大，需要缩小近似的范围； $\rho$ 太大，则实际减少的值大于近似减少的值，近似较小，需要扩大近似的范围。这样的话，就可以动态调整步长了。

通过近似指标，我们可以设定信赖区域的大小。当没有接近我们设定的阈值，则不断调整动态区域，直到找到好的近似结果。

当找到符合要求的近似结果后，就可以进行后续正常的迭代更新了。

因此，使用该信赖区域后，可以更新算法流程：

给定某个初始值$x_0$;
对于第 $k$ 次迭代,在高斯牛顿法的基础上加上信赖区域;

$min \frac{1}{2}||f(x_k)+J(x_k)^T\Delta x_k||^2, \qquad s.t \qquad ||D\Delta x_k||^2 \le \mu$ 其中,$\mu$ 是信赖半径, $D$ 位系数矩阵

计算近似指标$\rho$

$\rho = \frac{f(x+ \Delta x)-f(x)}{J(x)^T\Delta x}$

根据经验值,设定:

1). 若 $\rho \ge \frac{3}{4}$, 则设置$\mu = 2\mu$ ,跳转到第6步 2). 若 $\rho \le \frac{1}{4}$, 则设置$\mu = 0.5\mu$ ,跳转到第6步 3). 若 $\rho$ 大于设定的阈值,则跳转至第5步,求解$\Delta x_k$,令$\Delta x_{k+1}=x_k+\Delta x_k$

求解增量方程:$(H + \lambda I)\Delta x_k = g$ ;
若 $\Delta x_k$ 足够小,则停止迭代,否则,返回第2步.

至于增量方程的获取，可以通过拉格朗日函数来求解：

$min \frac{1}{2}||f(x_k)+J(x_k)^T\Delta x_k||^2, \qquad s.t \qquad ||D\Delta x_k||^2 \le \mu$

构建拉格朗日函数， $\lambda$ 是系数因子：

$L(\Delta x,\lambda) = \frac{1}{2}||f(x)+J(x)^T\Delta x||^2+\frac{\lambda}{2}(||D\Delta x||^2-\mu)$

这样的话，化简后求导就可以得到：

$J(x)f(x)+J(x)J^T(x)\Delta x + \lambda D^TD\Delta x=0$

我们化简后得到：

$(JJT+\lambda D^TD)\Delta x=-Jf$

在本文中，我们令 $H=JJ^T,g=-Jf$ 。在实际使用中，通常用 $I$ 来代替 $D^TD$ 。所以，公式就变为：

$(H+\lambda I)\Delta x_k=g$

这样，就可以得到对应的增量方程了。

代入算法流程中，最终就可以优化得到最小二乘问题的极小值了。

几种方法的总结与联系

我们已经知晓了四种优化的方法，分别是：

牛顿法： $H\Delta x=-J \quad s.t \quad H=f^{’’}(x_k),J=f{’}(x_k)$ 梯度下降法： $\Delta x = -\gamma J \quad s.t \quad J=f^{’’}(x_k)$ 高斯牛顿法： $H\Delta x = g \quad s.t \quad H=JJ^T,g=-Jf$ 列文伯格-马夸特法： $(H+\lambda I)\Delta x_k = g \quad s.t \quad H=JJ^T,g=-Jf$ 其实，这四种方法在最小二乘的问题求解中，也是有着联系的。

我们设定最小二乘问题为：

$minF(x)=\frac{1}{2}||f(x)||^2_2$

根据针对求解的是目标函数还是误差函数，可以将问题进行分类：

针对目标函数 $F(x)$ 优化

对于目标函数$F(x)$ 进行一阶泰勒展开：

$F(x_k+\Delta x_k) \approx F(x_k)+J(x_k)^T\Delta x_k$

此时，此时变成求最小值的问题，则：

$\Delta x^*_k=argmin(F(x_k)+J(x_k)^T\Delta x_k)$

故，对其求最小值，可以进行求一阶导数为0：

$\Delta x_k=-J(x_k)^T$

可以看到，如果增加一个步长 $\lambda$ ，此时的方法就是梯度下降法。

如果对目标函数 $\Delta x^*_k$ 其进行二阶泰勒展开：

$F(x_k+\Delta x_k) \approx F(x_k)+J(x_k)^T\Delta x_k+\frac{1}{2}\Delta x^T_kH(x_k)\Delta x_k$ 则，此时的增量方程为最小二乘问题：

$\Delta x^*_k=argmin(F(x_k)+J(x_k)^T\Delta x_k) + \frac{1}{2}\Delta x^T_kH(x_k)\Delta x_k$

则，为了求其最小值，对 [公式] 进行求导：

$J(x_k)+H(x_k)\Delta x_k=0 \to H*\Delta x = -J$

则此时的方法为牛顿法。

所以，如果从目标函数 $F(x)$ 入手的话，梯度下降法和牛顿法就是其一阶泰勒展开和二阶泰勒展开的求解方法。

针对误差函数 $f(x)$ 优化

上面正文部分的4和5，就是对误差函数的优化，可以得到两种方法：高斯牛顿法和列文伯格-马夸特法。

其中，列文伯格-马夸特法是在高斯牛顿法的基础上得来的。他们之间的联系，主要取决于参数 $\lambda$ ：

$\lambda$ 较大的时候，公式变为： $\lambda I \Delta x_k=g$ ，此时为梯度下降法 $\lambda$ 较小的时候，公式变为： $H\Delta x_k=g$ ，此时为高斯牛顿法。所以， LM 法可以在一定程度上避免线性方程组的系数矩阵的非奇异和病态的问题，从而得到更精准，更稳定的增量 $\Delta x_k$ 。

通过上面内容，我们知道了牛顿法，梯度下降法，高斯牛顿法和列文伯格-马夸特法的区别和联系了。

不管是什么方法，初始参数的选取很重要，给一个好的参数，可以减少迭代次数，更快的收敛，从而减少很多的计算量。

在实际的使用中，可以根据具体的情况来最终决定，到底要使用那种方法来进行优化求解。